复习时看到一个有趣的问题,遂记下来思考过程。
有一个点对点链路,长度为 $20000\ km$ ,数据发送的速率是 $1\ kbit/s$ ,要发送的数据 $100\ bit$。数据在此链路上的传播速度为 $2\times10^8\ m/s$ 。假定我们可以看见线路上传输的比特,试画出我们看到的线路上的比特(画两个图,一个在 $100\ bit$ 刚刚发送时,一个是再经过 $0.05\ s$ 后)。
首先我们考虑发送 $100\ bit$ 的时间。根据公式可计算,
$$ t = \frac{100\ bit}{1\ kbit/s} = 0.1\ s $$
如果把比特想象成在链路中移动的“粒子”,那么经过 $0.1\ s$ 后,这束比特的最后一枚粒子已经送离设备,且位于链路的起点处。题目中指出,数据在此链路上的传播速度为 $2×10^8\ m/s$ ,则可计算最开始送出的第一枚粒子已经移动的距离为
$$ s_1 = 0.1\ s \times 2\times10^8\ m/s = 2\times10^7\ m=2000\ km $$
正巧链路长度也为 $20000\ km$ ,即连续送出的比特粒子,第一枚位于链路终点,最后一枚位于链路起点。则此时链路中已布满了比特粒子。
在链路中,比特粒子移动的速度由传播速度决定。则 $0.05\ s$ 后,最后一枚粒子行进的路程为
$$ s_2 = 0.05\ s \times 2\times10^8\ m/s = 2\times10^7\ m=1000\ km $$
为链路长度 $20000\ km$ 的一半。则此时最后一枚粒子位于链路的中央,前面的粒子的一半已陆续离开链路终点。则我们可以画一张粗略的图,表示在 $100\ bit$ 刚刚发送完时和再过 $0.05\ s$ 后。
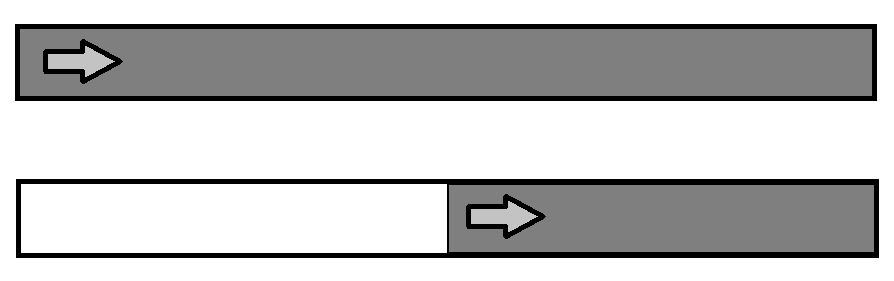
图的上方是刚发送完100比特时,管道内布满了比特;下方是 0.05 秒后,有一半的空间已经被空了出来。